(Total Views: 1629)
Posted On: 12/12/2020 9:11:28 AM
Post# of 158026

So we are back to analyzing the full enrollment trial, which imo makes sense due to the acceleration on recruitment.
Why does it make sense ??? Please refer to the table below. In the second section we can see that, needing a p-value of around 0.01 ( O'Brian criteria), Post-hoc analysis would indicate a power of 76.4%.
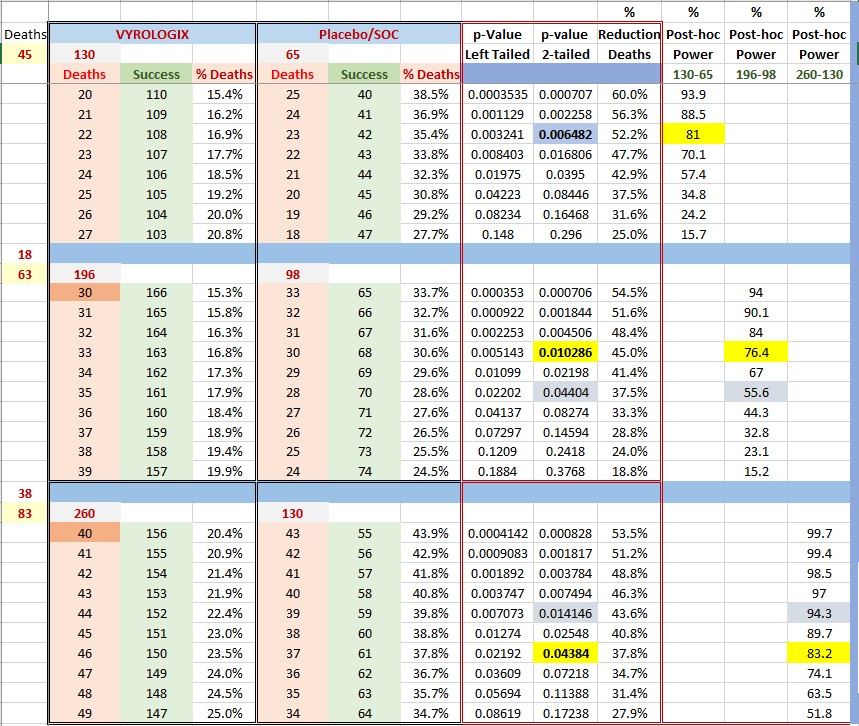
However, if we go full enrollment now we will need a p-value of 0.05 and our power will be larger than 80% (in my example we have 83.2% and a p-value of 0.0438).
Some conclusions can be drawn: meeting the primary point will be easier at full enrollment. Also, if we take into account the number of patients required, the trial was looking at a power of 80% not 90%.
For example, if we were to have a power of 90% we would need app. 516 patients (all other conditions being equal). Also, note from the table that what we are gaining is a power of 27.6% (83.2%-55.6%) by completing the trial. Please note: all these analysis are Post-hoc.
Now, to the important stuff. I assumed that the rate of deceases was smaller (38 vs 45) for the second half. I might be completely wrong (in number of deaths) and the numbers, of course will be different. However this gives us an idea that if we have a reduction of deaths of app.37.8% we are golden. That is, if the total number of deaths is 83 and Vyrologix/SOC ratio is 46/37.
Regardless, I still believe that even a 48/35 ratio (31.4% reduction) should be approved immediately . If my math is correct, that would mean close to 93000 lives saved as of today.
Isn't that enough ?????
PD: The table makes several assumptions and calculation methodologies, please use it only for broad reference purposes, also, it assumes numbers of deaths, information I don't possess. These can, and will probably change.
Why does it make sense ??? Please refer to the table below. In the second section we can see that, needing a p-value of around 0.01 ( O'Brian criteria), Post-hoc analysis would indicate a power of 76.4%.

However, if we go full enrollment now we will need a p-value of 0.05 and our power will be larger than 80% (in my example we have 83.2% and a p-value of 0.0438).
Some conclusions can be drawn: meeting the primary point will be easier at full enrollment. Also, if we take into account the number of patients required, the trial was looking at a power of 80% not 90%.
For example, if we were to have a power of 90% we would need app. 516 patients (all other conditions being equal). Also, note from the table that what we are gaining is a power of 27.6% (83.2%-55.6%) by completing the trial. Please note: all these analysis are Post-hoc.
Now, to the important stuff. I assumed that the rate of deceases was smaller (38 vs 45) for the second half. I might be completely wrong (in number of deaths) and the numbers, of course will be different. However this gives us an idea that if we have a reduction of deaths of app.37.8% we are golden. That is, if the total number of deaths is 83 and Vyrologix/SOC ratio is 46/37.
Regardless, I still believe that even a 48/35 ratio (31.4% reduction) should be approved immediately . If my math is correct, that would mean close to 93000 lives saved as of today.
Isn't that enough ?????
PD: The table makes several assumptions and calculation methodologies, please use it only for broad reference purposes, also, it assumes numbers of deaths, information I don't possess. These can, and will probably change.
