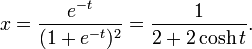Hubbert Curve
Shape
The prototypical Hubbert curve is a probability density function of a logistic distribution curve. It is not a gaussian function (which is used to plot normal distributions ), but the two have a similar appearance. The density of a Hubbert curve approaches zero more slowly than a gaussian function:
The graph of a Hubbert curve consists of three key elements:
- a gradual rise from zero resource production that then increases quickly
- a " Hubbert peak ", representing the maximum production level
- a drop from the peak that then follows a steep production decline.
The actual shape of a graph of real world production trends is determined by various factors, such as development of enhanced production techniques, availability of competing resources, and government regulations on production or consumption. Because of such factors, real world Hubbert curves are often not symmetrical.
Application
Peak oil
Using the curve, Hubbert modeled the rate of petroleum production for several regions, determined by the rate of new oil well discovery, and extrapolated a world production curve. [ 1 ] The relative steepness of decline in this projection is the main concern in peak oil discussions. This is because a steep drop in the production implies that global oil production will decline so rapidly that the world will not have enough time to develop sources of energy to replace the energy now used from oil, possibly leading to drastic social and economic impacts.
Other resources
Hubbert models have been used to predict the production trends of various resources, such as natural gas (Hubbert's attempt in the late 1970's resulted in an inaccurate prediction that natural gas production would fall dramatically in the 1980's), Coal , fissionable materials , Helium , transition metals (such as copper ), and water . At least one researcher has attempted to create a Hubbert curve for the whaling industry and caviar, [ 2 ] while another applied it to cod . [ 3 ]